星型を描くと、特別な比$1:\ph$が現れる。
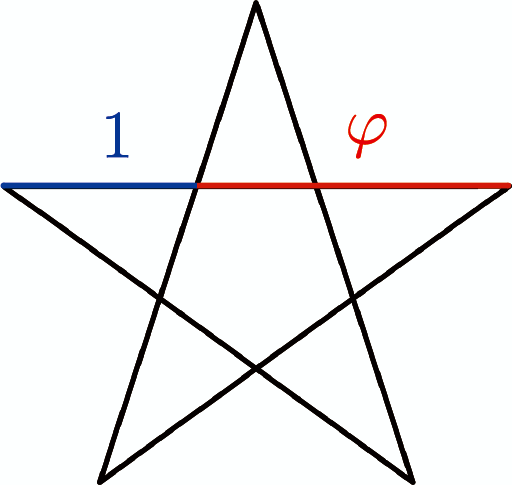
これが、あの黄金比。
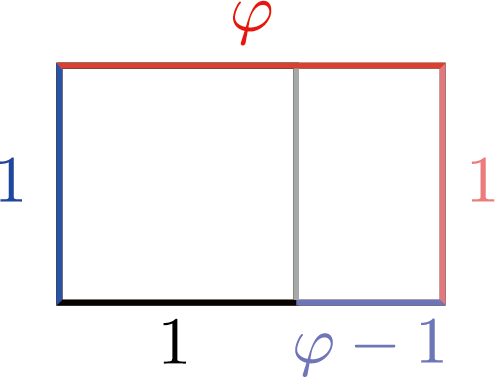
黄金比は、次の性質を満たす比として定まる。
縦横が黄金比の長方形から正方形を取り去ると、残った長方形も縦横が黄金比になる。
$1:\ph = (\ph -1) :1$
$\ph$の正確な値は$\f{1+\sq{5}}{2}$。およそ1.618である。
発音のタイミングと周波数を黄金比で演奏してみた。
黄金比には、面白い性質がいろいろある。
たとえば、5.でやったフィボナッチ数列。
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…
この隣り合う項の比をとってみると、
$\f{1}{1} = 1,~~ \f{2}{1} = 2,~~ \f{3}{2} = 1.5,~~ \f{5}{3} = 1.666…, ~~\f{8}{5} = 1.6$
$\ph$に近づいていく。
こんなきれいな表し方も。
$\ph = \sq{1+\sq{1+\sq{1+ \sq{1+ \dots}}}}$
$\ph = 1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\dots}}}}}$
A special ratio $1:\ph$ appears in a star shape.

This is what you call the golden ratio.
The golden ratio is characterized by a special property.
Draw a golden rectangle, that is, a rectangle with side lengths in the golden ratio. Take away a square. Then, the remaining shape is again a golden rectangle.
$1:\ph = (\ph -1) :1$
The exact value of $\ph$ is $\f{1+\sq{5}}{2}$. It is about 1.618.

We converted the golden ratio into timing and frequencies.
The golden ratio has lots of interesting properties.
For example, it is related to the Fibonacci sequence in [5. Fibonacci].
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…
Take the ratios of two successive terms.
$\f{1}{1} = 1,~~ \f{2}{1} = 2,~~ \f{3}{2} = 1.5,~~ \f{5}{3} = 1.666…, ~~\f{8}{5} = 1.6$
The ratio approaches $\ph$.
$\ph$ also has such beautiful expressions.
$\ph = \sq{1+\sq{1+\sq{1+ \sq{1+ \dots}}}}$
$\ph = 1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\dots}}}}}$
Un ratio spécial $1 :\ph$ apparaît en forme d’étoile.

C’est ce que vous appelez le nombre d’or.
Le nombre d’or est caractérisé par une propriété particulière.
Dessinez un rectangle d’or, c’est-à-dire un rectangle dont les côtés mesurent le nombre d’or. Enlevez un carré. Ensuite, la forme restante est à nouveau un rectangle d’or.
$1:\ph = (\ph -1) :1$
La valeur exacte de $\ph$ est $\f{1+\sq{5}} {2} $. Il est environ 1,618.

Nous avons converti le nombre d’or en timing et en fréquences.
Le nombre d’or a beaucoup de propriétés intéressantes.
Par exemple, il est lié à la suite de Fibonacci dans [5. Fibonacci].
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…
Prenons les ratios de deux termes successifs.
$\f{1}{1} = 1,~~ \f{2}{1} = 2,~~ \f{3}{2} = 1,5,~~ \f{5}{3} = 1,666…, ~~\f{8}{5} = 1,6$
Le ratio approche $\ph$.
$\ph$ a aussi de si belles expressions.
$\ph = \sq{1+\sq{1+\sq{1+ \sq{1+ \dots}}}}$
$\ph = 1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\dots}}}}}$
試聴は下記よりTry from belowEssayez d’en bas

